AVLs

AVL trees

AVL Trees are sub classification of BSTs.

AVL Properties and Efficiency

• Height(node) = max{Height(left), Height(right)} + 1

  • Base cases: Height(leaf) = 0, Height(null) = -1

• BalanceFactor(node) = Height(left) - Height(right)

• AVLs store heights and balance factors to make calculations O(1) as opposed to O(n)

Definition of Unbalanced

• Node is unbalanced if |BF| > 1
• Node is balanced if BF = -1, 0, 1

Rotaions

Rotations are operations performed in AVL trees to maintain and restore balance.

In AVL trees, there are two fundamental types of rotations.

• Single rotation
  
  • Left rotation
    
    
    
    
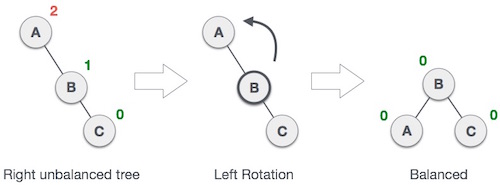
  • Internet source: AVL Tree Insertion, Rotation, and Balance Factor Explained. Retrieved from https://www.freecodecamp.org/news/avl-tree-insertion-rotation-and-balance-factor/ (Accessed on May 24, 2023).
    
    

    Pseudocode leftRotation(Node A)
    1. Node B <- A's right child
    2. A's right child <- B's left child
    3. B's left child <- A
    4. Update the height & BF of A
    5. Update the height & BF of B
    6. Return B
    

  • Right rotation
    
    
    
    
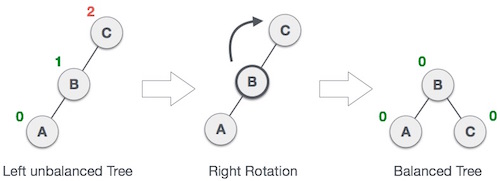
  • Internet source: AVL Tree Insertion, Rotation, and Balance Factor Explained. Retrieved from https://www.freecodecamp.org/news/avl-tree-insertion-rotation-and-balance-factor/ (Accessed on May 24, 2023).
    
    

    Pseudocode rightRotation(Node C)
    1. Node B <- C's left child
    2. C's left child <- B's right child
    3. B's right child <- C
    4. Update the height & BF of C
    5. Update the height & BF of B
    6. Return B
    

• Double rotation

• Internet source: AVLs. AVL Rotations. Retrieved from Edx Data Structures & Algorithm (Accessed on May 25, 2023).